Momen inersia adalah kelembaman rotasi suatu benda yang bergerak berputar. Seperti botol yang penuh berisi penuh air akan mampu berputar lebih stabil dan lama dibandingkan dengan botol saya yang kosong

Rumus:
I = M.R²
Atau:
I = Σ(M.R²)
keterangan :
I = momen inersia (kg.m²)
M = massa (kg)
R = jari² /jarak massa ke poros (m)
contoh soal momen inersia benda titik:
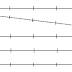
1. perhatikan gambar patikel partikel ang dihubungkan dengga batang tak bepatikel partikelmassa berikut:
2. perhatikan gambar patikel partikel berikut:
Hitung besar momen inersia sistem partikel di atas. Jika :
a. Diputar dengan poros pada sumbu x
b. Diputar dengan poros pada sumbu y
Penyelesaian dan pembahasan:
a. Jika diputar dengan poros sumbu x maka semua partikel yang berada pada sumbu x bernilai nol (I = 0) karena R = 0 . Sehingga :
I = ΣM.R² = 2.3² + 2.3² = 36 kg.cm²
b. Jika diputar dengan poros sumbu y maka semua partikel yang berada pada sumbu x bernilai nol (I = 0) karena R = 0 . Sehingga :
I = ΣM.R² = 1.2² + 3.2² + 2.4² + 1.6²
I = 4 + 12 + 32 + 36 = 84 kg.cm²
Rumus:
1. Silinder pejal dengan poros di tengah
I = 1/2.M.R²
2. Silinder berongga dengan poros di tengah
I = M.R²
3. Bola pejal dengan poros ditengah
I = 2/5 . M.R²
4. Bola berongga dengan poros ditengah
I = 2/3. M.R²
3. Batang homogen panjang dengan poros ditengah
I = 1/12 . M.L²
4. Batang homogen panjang dengan poros di ujung
I = 1/3 . M.L²
Keterangan :
L = penjang batang (m)
R = jari - jari benda tegar
Rumus:
I = Ipm + m.d²
Keterangan :
Ipm = rumus momen inersia benda tegar dengan poros ditengah atau pusat massa
d = jarak poros ke titik tegah
Contoh soal teorema sumbu paralel:
Sebuah tongkat pramuka berbentuk silinder panjang homogen bermassa 2 kg dan panjang 2,4 meter. Hitung besar momen inersia batang tersebut jika diputar dengan poros:
A. Di salah satu ujung
B. Di tengah / pusat massa
C. Pada titik 40 cm dari salah satu ujung batang
Pembahasan dan penyelesaian:
A) momen inersia batang homogem di ujung
I = 1/3 .M.L² = 1/3. 2 . 2,4² = 3,84 kg.m²
B) momen inersia batang homogem di tengah / pusat massa
I = 1/12 . M.L² = 1/12 . 2 . 2,4² = 0,24 kg.m²
C) Dari soal B didapat Ipm
I = Ipm + m.d²
I = 0,24 + 2. 0,8²
I = 0,25 + 1,28 = 1,53 kg.m²
untuk 64 contoh soal dan pembahasan lebih lengkap bisa di buka pada kolom "pembahasan soal fisika kelas XI"
atau link berikut:
momen inersia benda titik / partikel

Rumus:
I = M.R²
Atau:
I = Σ(M.R²)
keterangan :
I = momen inersia (kg.m²)
M = massa (kg)
R = jari² /jarak massa ke poros (m)
contoh soal momen inersia benda titik:
1. perhatikan gambar patikel partikel ang dihubungkan dengga batang tak bepatikel partikelmassa berikut:
Hitung besar momen inersia jika sistem partikel diputar dengan poros di partikel biru!
Penyelesaian dan pembahasan:
diketahui:
- bola merah (m = 1 kg . R = 6cm)
- bola kuning (m = 2 kg . R = 4 cm)
- bola hijau (m = 3 kg . R = 2 cm)
- bola biru (m = 2 kg . R = 0 )
- Bola ungu (m = 1 kg . R = 2 cm)
jawab:
I = ΣM.R²
I = 1 . 6² + 2.4² + 3.2² + 2.0 + 1.2²
I = 36 + 32 + 12 + 0 + 4
I = 84 kg.cm²
Hitung besar momen inersia sistem partikel di atas. Jika :
a. Diputar dengan poros pada sumbu x
b. Diputar dengan poros pada sumbu y
Penyelesaian dan pembahasan:
a. Jika diputar dengan poros sumbu x maka semua partikel yang berada pada sumbu x bernilai nol (I = 0) karena R = 0 . Sehingga :
I = ΣM.R² = 2.3² + 2.3² = 36 kg.cm²
b. Jika diputar dengan poros sumbu y maka semua partikel yang berada pada sumbu x bernilai nol (I = 0) karena R = 0 . Sehingga :
I = ΣM.R² = 1.2² + 3.2² + 2.4² + 1.6²
I = 4 + 12 + 32 + 36 = 84 kg.cm²
momen inersia benda tegar
Benda tegar adalah benda yang memiliki massa dan bentuk tertentuRumus:
1. Silinder pejal dengan poros di tengah
I = 1/2.M.R²
2. Silinder berongga dengan poros di tengah
I = M.R²
3. Bola pejal dengan poros ditengah
I = 2/5 . M.R²
4. Bola berongga dengan poros ditengah
I = 2/3. M.R²
3. Batang homogen panjang dengan poros ditengah
I = 1/12 . M.L²
4. Batang homogen panjang dengan poros di ujung
I = 1/3 . M.L²
Keterangan :
L = penjang batang (m)
R = jari - jari benda tegar
Teorema sumbu paralel
I = Ipm + m.d²
Keterangan :
Ipm = rumus momen inersia benda tegar dengan poros ditengah atau pusat massa
d = jarak poros ke titik tegah
Contoh soal teorema sumbu paralel:
Sebuah tongkat pramuka berbentuk silinder panjang homogen bermassa 2 kg dan panjang 2,4 meter. Hitung besar momen inersia batang tersebut jika diputar dengan poros:
A. Di salah satu ujung
B. Di tengah / pusat massa
C. Pada titik 40 cm dari salah satu ujung batang
Pembahasan dan penyelesaian:
A) momen inersia batang homogem di ujung
I = 1/3 .M.L² = 1/3. 2 . 2,4² = 3,84 kg.m²
B) momen inersia batang homogem di tengah / pusat massa
I = 1/12 . M.L² = 1/12 . 2 . 2,4² = 0,24 kg.m²
C) Dari soal B didapat Ipm
I = Ipm + m.d²
I = 0,24 + 2. 0,8²
I = 0,25 + 1,28 = 1,53 kg.m²
untuk 64 contoh soal dan pembahasan lebih lengkap bisa di buka pada kolom "pembahasan soal fisika kelas XI"
atau link berikut:



















2 Comments
D = jarak poros dari pusat.
Disoal diketahui jarak poros dari ujung sehingga bisa kita hitung:
D = 1,2 m - 40 cm = 1,2 m - 0,4 m = 0,8 m